RSA解密正确性证明_国科大网安二班的博客-CSDN博客https://blog.csdn.net/weixin_article/details/:~:text=RSA%E,A,A,E,AF%E,AD%A,E,A,AE%E,A,E,AF%E,%E,E,%%E,BF%B,E,B,E,B,RSA%E,AF%E。第一个场景:战场上,B要给A传递一条消息,内容为某一指令。RSA的加密过程如下:(A生成一对密钥(公钥和私钥),私钥不公开,A自己保留。公钥为公开的,任何人可以获取。(A传递自己的公钥给B,B用A的公钥对消息进行加密。(A接收到B加密的消息,利用A自己的私钥对消息进行解密。
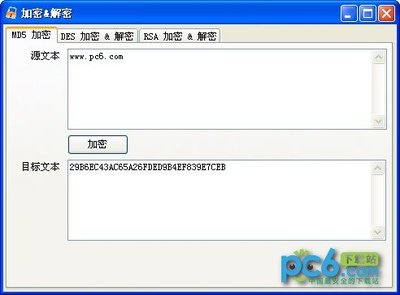
这里细节不多展开阐述,涉及到很多数学原理,如大数的质因数分解等,感兴趣的可以找找李永乐等网上比较优秀的科普。这篇文章只是java原生实现的加解密例子。至于其他的如md,hash等,如果从主观可读的角度来说,也可以称为加密。如下的示例是使用Java原生实现RSA的加密解密,包括用公钥加密,然后私钥解密。RSA加密是一种非对称加密。可以在不直接传递密钥的情况下,完成解密。这能够确保信息的安全性,避免了直接传递密钥所造成的被破解的风险。是由一对密钥来进行加解密的过程,分别称为公钥和私钥。两者之间有数学相关,该加密算法的原理就是对一极大整数做因数分解的困难性来保证安全性。通常个人保存私钥。
RSA是一种块加密的算法,所以对于明文需要将他们分成固定的块长度,考虑到输入的数据长度的问题,所以加解密的填充有好几种:无填充,就是直接对明文进行加密PKCS,将数据长度分成密钥长度-yte,比如密钥是,it,那么长度就是,,ytes,具体的格式:先填。如importgmpy,printgmpy,invert(可求得,,逆为,扩展欧几里得算法基于欧几里得算法,能够求出使得ax by=gcd(a,b)的一组x,y。常见攻击方式实践准备工具pythongmpy,libnum库yafuRSATool,,exeRSA解密若已知私钥d。
RSA解密工具
这里细节不多展开阐述,涉及到很多数学原理,如大数的质因数分解等,感兴趣的可以找找李永乐等网上比较优秀的科普。这篇文章只是java原生实现的加解密例子。至于其他的如md,hash等,如果从主观可读的角度来说,也可以称为加密。如下的示例是使用Java原生实现RSA的加密解密,包括用公钥加密,然后私钥解密。RSAPKCS,ignatureDeformatterRSADeformatter=newRSAPKCS,ignatureDeformatter(rsa,;RSADeformatter.SetHashAlgorithm(
感谢您的来访,获取更多精彩文章请收藏本站。













暂无评论内容